"That is why during the bifurcation, the unitary strength remains the same – the subjective and objective having equal value in strength during the phase of reduction." [Microvita and Cosmology]
"Waves are created when microvita move through the media of inferences. Inferences are the major waves, but sub-waves are created in them by moving microvita. The major waves function as the controlling waves for the sub-waves." [Questions and Answers on Microvita – Section H]
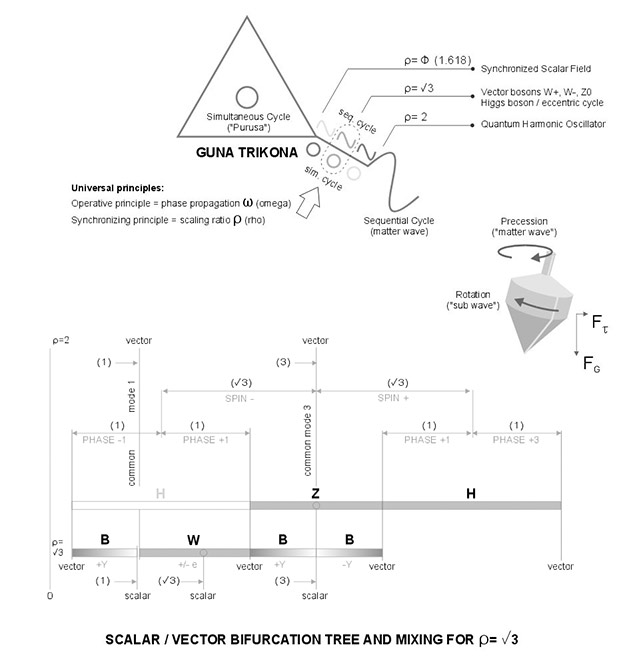
In the Standard Model of elementary particles and interactions, the vector- or intermediate bosons (force particles) connect the hidden realm of the weak nuclear force with the visible world of electromagnetism. This process is called electroweak symmetry breaking. It appears to be the quantum physics equivalent of the wave breaking out of the gunatrikona in guna creation theory, or "bifurcation" in microvita theory. The vector bosons have distinct masses which can be measured and to some extend be calculated, but there is currently no generally accepted theory. The new theorem of a synchronous scalar field (of which microvita are the proposed quanta), provides a theoretical framework for the real function of the vector bosons, and the calculation of their masses. Below images provide a brief synopsis of the main principles.
click to enlarge
Simplified explanation
The idea is that during the linear flow of expression, the hidden, simultaneous cycle ("Purusa")
vanishes only gradually, whereas the sequential cycle or matter wave gradually increases. The actual breakout ("eigenstate" [QFT], "silver lining between matter and abstract" [PRS])
occurs during the resonant mixing of scalar and vector modes.
The spinning top is a simple mechanical mataphor of how the sub-waves and matter ("major") wave mix under the influence of internal and external forces. Note the single parameters representing the Operative and Synchronizing (phil.: cognitive) Principles.
Bifurcation tree
Above image shows the resonant mixing, optimized at rho = V3, reproduced by means of a bifurcation tree. The masses of the intermediary vector bosons form the signature of this resonant state or eccentric cycle (phil.: "nada").
Common modes vs. charge coupling
The common modes (1 to 3) form the backbone of the synchronous symmetry break. It means that a specific component (eigen value) of an eigenstate is aligned with the external or matter wave. General common mode 1 exists throughout the scaling gauge and controls the fundamental alignment of the scalar and fields. Special common mode 2 (not shown here) is exclusive for rho=Phi and controls the expansion of the field. Special common mode 3 is exclusive for rho=V3 and controls the resonance. Common modes 1 and 3 split a primary vector boson into a hypercharge- and an electrical component. Vice versa, charge coupling involves the indirect, progressive alignment of the resonant and external fields. Electrical coupling requires weak isospin, so this must be the W-boson. In fact there are two identical H-fields, one of which dissociates into a B- plus W-boson. Similarly, the Z-boson resolves into two opposite B-bosons and is it's own anti-particle. The stationary, uncharged H-boson has no weak isospin and is considered a pure scalar boson.
Physical effects
The B-bosons represent the unit of electroweak hypercharge inbetween the resonant vector- and common mode scalar modes.
Vice versa, the W-boson carries the electrical charge between the resonant scalar- and common mode vector modes. After the charge-splitting, the electrical charge is scaled by rho=V3 / rho=2 times the weak hypercharge.
The H- Z- and W-bosons interacting inbetween (resonant) vector modes carry no hypercharge. Their masses are proportional to the B-boson (Synchronizing Principle).
The W- and Z- bosons have weak isospin-1 (analogous to the photon's EM-isospin), pivoted on the resp. scalar modes ("Operative Principle").
Philosophical analogies
|
|
|
|
Operative
Principle, physical
|
Operative Principle, theor. |
Operative Principle, phil.
|
Synchronous
Electroweak
Symmetry
Breaking
|
|
Quantum
Harmonic
Oscillator
|
|
Energy;
phase propagation (omega)
|
Sequential cycle |
|
Electroweak
interaction or mixing
|
|
Vector bosons
W+, W-, Z0
(mass)
|
Resonant or eccentric cycle |
|
Synchronous
Scalar
Self-interaction
|
|
|
Simultaneous cycle |
|
|
|
